Section outline
-
Funktionen sind ... -
Es kann nur einen geben!
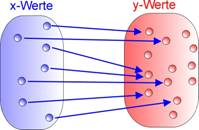
Funktionen sind eindeutige Zuordnungen!
Jeder Tageszeit wird eine bestimmte Temperatur zugeordnet.
Jedem Wert x einer bestimmten Menge wird eindeutig ein bestimmter Wert y einer anderen Menge zugeordnet.
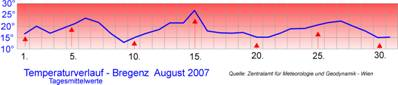
Zwei x-Werte können zwar den gleichen y-Wert haben, aber zwei verschiedene y-Werte dürfen nicht den gleichen x-Wert haben.
Es kann nicht sein, dass es zu einem bestimmten Zeitpunkt an einem bestimmten Ort zwei verschiedene Temperaturen gibt.
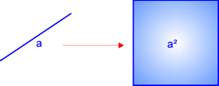
Jeder Seitenlänge eines Quadrats ein bestimmter Flächeninhalt.
Ein Quadrat mit der Seitenlänge a kann nicht zwei verschiedene Flächeninhalte haben.
Jeder Warenmenge wird ein bestimmter Preis zugeordnet.
Man kann für einen bestimmten MP3-Player in einem bestimmten Geschäft zur gleichen Zeit
nicht zwei verschiedene Preise bezahlen.
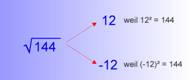
„Aus eins mach zwei“ ist keine Funktion!
Wenn man aus einer Zahl die Quadratwurzel zieht, erhält man zwei verschiedene Lösungen – daher ist dies keine eindeutige Zuordnung und auch keine Funktion.
Man kann sich eine Funktion auch als Vorschrift für eine Maschine denken, bei der für jede Eingabe genau ein Wert heraus kommt.
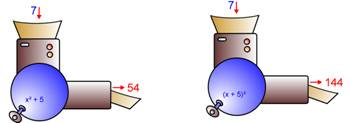
Die eingegebene Zahl wird quadriert und mit 5 addiert.
oder: Die eingegebene Zahl wird um 5 vergrößert und das Ergebnis quadriert.Quelle: http://www.ph-linz.at/staff/boe/algebra/funktionen.htm